신장 트리란?
Spanning Tree, 또는 신장 트리라고 불린다.
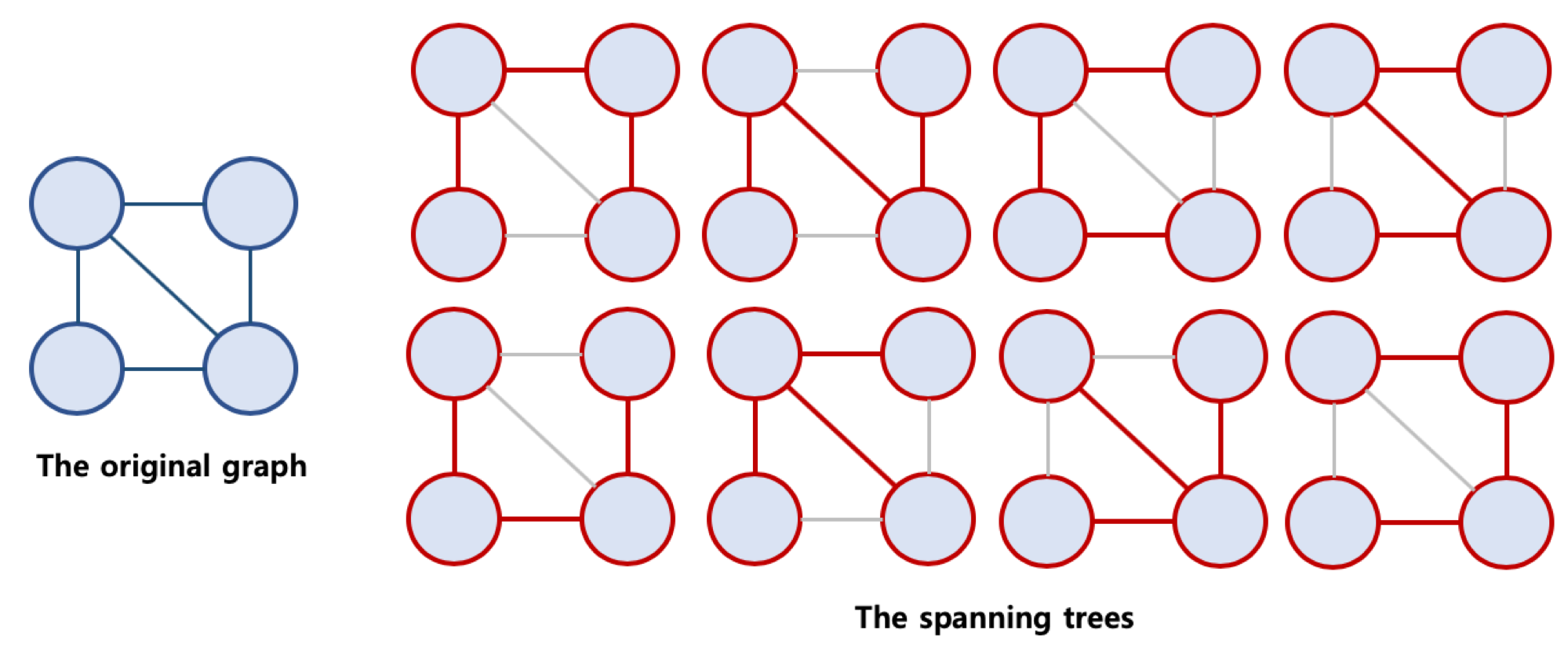
- 원래 그래프의 모든 노드가 연결되어 있으면서, 트리의 속성을 만족하는 그래프이다.
* 신장 트리의 조건
- 본래 그래프의 모든 노드를 포함해야 한다.
- 모든 노드가 서로 연결되어 있다.
- 트리의 속성을 만족시킨다.(사이클이 존재하지 않음)
최소 신장트리
- MST(Minimum Spanning Tree) 라고 불린다.
- 가능한 Spanning Tree 중에서 간선의 가중치 합이 최소인 Spanning Tree 를 지칭한다.
* 최소 신장 트리 알고리즘
- 그래프에서 최소 신장 트리를 찾을 수 있는 알고리즘이 존재한다.
- 대표적인 최소 신장 트리 알고리즘으로 크루스칼 알고리즘과 프림 알고리즘이 있다.

크루스칼 알고리즘
1. 모든 정점을 독립적인 집합으로 만든다.
2. 모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.
3. 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다.
(최소 신장 트리는 사이클이 없으므로 사이클이 생기지 않도록 하는것)
- 탐욕 알고리즘을 기초로 한다.(당장 눈앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
4. 최종적으로 모든 노드들을 연결시킨다.(마지막으로 연결된 노드 이후로 마지막 노드보다 가중치가 더 큰 노드가 있을 수 있으나, 어차피 노드들이 다 연결되어 있는 상태이므로 고려하지 않는다.)
* 최소 신장 트리를 구할 때의 핵심은 사이클이 생기지 않도록 하는 것이다. 그렇기 때문에 특정 노드를 선택했을 때 그래프(또는 트리) 에서 전체적으로 사이클이 생기는지, 생기지 않는지를 체크해 주는 기법이 필요하다.
* 여기서 Union Find 알고리즘을 이용하면 그래프(트리) 에서 사이클이 생기는지 생기지 않는지 판별해줄 수 있다.


Union Find 알고리즘
Disjoint Set 을 표현할 때 사용하는 알고리즘으로 트리 구조를 활용하는 알고리즘이다.
간단하게 말해서, 노드들 중에 연결된 노드를 찾거나, 노드들을 서로 연결 할 때(합칠 때) 사용한다.
* Disjoint Set 이란
- 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
- 공통원소가 없는(서로소) 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조를 의미한다.
- Disjoint Set = 서로소 집합 자료구조
Union Find 의 알고리즘 동작 순서
1. 초기화 : n 개의 원소가 개별 집합으로 이뤄지도록 초기화
2. Union : 두 개별 집합을 하나의 집합으로 합친다, 두 트리를 하나의 트리로 만든다.
3. Find : 여러 노드가 존재할 때, 두 개의 노드를 선택해서 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소(즉, 루트 노드) 를 확인한다.(사이클 존재 여부 체크)
Union Find 알고리즘에서 고려해야 할 점
- Union 순서에 따라서 최악의 경우 연결 리스트와 같은 형태가 될 수 있다.
- 이 때는 Find/Union 시 계산량이 O(N) 이 될 수 있으므로, 해당 문제를 해결하기 위해 union-by-rank, path compression 기법을 사용한다.
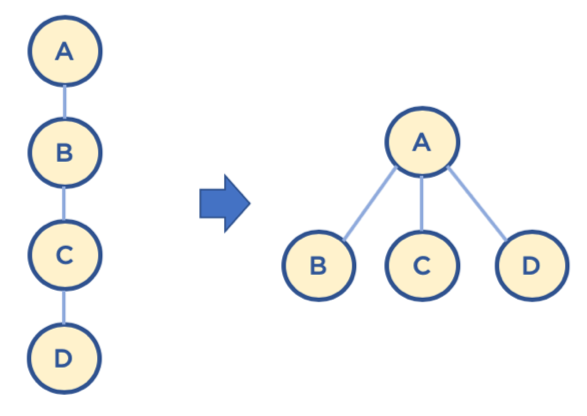
union-by-rank 기법
- 각 트리에 대해 높이(rank) 를 기억해두고, union 시 두 트리의 높이(rank) 가 다르면 높이가 작은 트리를 높이가 큰 트리에 붙인다.
- 즉, 높이가 큰 트리의 루트 노드가 합친 집합의 루트 노드가 된다.
- 높이가 h-1 인 두 개의 트리를 합칠 때는(높이가 동일한 두 개의 트리) 한 쪽의 트리 높이를 1 증가시켜주고, 다른 쪽의 트리를 해당 트리에 붙여준다.
- 초기화 시 모든 원소의 높이(rank) 가 0 인 개별 집합인 상태에서, 하나씩 원소를 합칠 때 union-by-rank 기법을 사용한다면,
- 높이가 h 인 트리가 만들어지려면 높이가 h-1 인 두 개의 트리가 합쳐져야 한다.
- 높이가 h-1 인 트리를 만들기 위해 최소 n 개의 원소가 필요하다면, 높이가 h 인 트리가 만들어지기 위해서는 최소 2n 개의 원소가 필요하다.
- 따라서 union-by-rank 기법을 사용하면 union/find 연산의 시간복잡도는 O(N) 이 아닌, O(logN) 으로 낮출 수 있다.
path compression 기법
- Find 를 실행한 노드와 거쳐간 노드를 모두 다 루트에 다이렉트로 연결하는 기법
- Find 를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있다.
자바로 직접 구현해보자.
- Edge.java
public class Edge implements Comparable<Edge>{
private String mainNode;
private String connectNode;
private int value;
public Edge(String mainNode, String connectNode, int value) {
this.mainNode = mainNode;
this.connectNode = connectNode;
this.value = value;
}
public String getMainNode() {
return mainNode;
}
public String getConnectNode() {
return connectNode;
}
public int getValue() {
return value;
}
// 가중치 기준 정렬을 위한 메소드 구현
@Override
public int compareTo(Edge edge) {
return value - edge.getValue();
}
}
- MSTmain.java
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashMap;
import java.util.List;
public class MSTmain {
// 각 노드의 부모 노드에 대한 정보 저장, 루트 노드일 경우 부모 노드는 자기 자신이다.
static HashMap<String, String> parent = new HashMap<String, String>();
// 트리 상에서 각 노드의 높이 정보를 적재한다.
static HashMap<String, Integer> rank = new HashMap<String, Integer>();
public static void main(String[] args) {
String[] nodeArray = {"A", "B", "C", "D", "E", "F", "G"};
Edge[] edges = {
new Edge("A", "B", 7),new Edge("A", "D", 5),new Edge("B", "A", 7),
new Edge("B", "C", 8),new Edge("B", "D", 9),new Edge("B", "E", 7),
new Edge("C", "B", 8),new Edge("C", "E", 5),new Edge("D", "A", 5),
new Edge("D", "B", 9),new Edge("D", "E", 7),new Edge("D", "F", 6),
new Edge("E", "B", 7),new Edge("E", "C", 5),new Edge("E", "D", 7),
new Edge("E", "F", 8),new Edge("E", "G", 9),new Edge("F", "D", 6),
new Edge("F", "E", 8),new Edge("F", "G", 11),new Edge("G", "E", 9),
new Edge("G", "F", 11)
};
List<Edge> mst = new ArrayList<Edge>();
for(String node : nodeArray) {
makeSet(node); // 초기화
}
Arrays.sort(edges); // 가중치 기준으로 오름차순 정렬
// 사이클 없는 간선만 연결
for(Edge edge : edges) {
int weight = edge.getValue();
String nodeV = edge.getMainNode();
String nodeU = edge.getConnectNode();
if(!find(nodeV).equals(find(nodeU))) {
// 루트 노드가 같지 않을 경우 두 트리를 하나로 합친다.
union(nodeV, nodeU);
mst.add(edge);
}
}
mst.stream().forEach(x -> System.out.println(x.getValue() + " " + x.getMainNode() + " " + x.getConnectNode()));
}
// 높이가 같거나 다른 두 개의 트리를 합치는 메소드
private static void union(String nodeV, String nodeU) {
String root1 = find(nodeV);
String root2 = find(nodeU);
// union-by-rank 기법 활용
// 한 쪽 노드의 트리의 높이가 다른 노드 트리의 높아보다 높은 경우
if(rank.get(root1) > rank.get(root2))
// 높이가 낮은 트리를 높이가 높은 트리에 병합(부모 노트 재설정)
parent.put(root2, root1);
else {
// root2 의 높이가 반대로 더 높은 경우
parent.put(root1, root2);
// 두 트리의 높이가 같은 경우
if(rank.get(root1) == rank.get(root2))
rank.put(root2, rank.get(root2)+1); // root2 트리의 높이를 1 올려준다.
}
}
// 루트 노드를 찾는 메소드 - path compression 기법을 사용한다.
private static String find(String node) {
// 현재 노드가 루트 노드가 아닐 경우
if(parent.get(node) != node)
parent.put(node, find(parent.get(node)));
// 재귀를 통해 최종적으로 루트 노드를 찾아온다.
return parent.get(node);
}
// 초기화 메소드 : 모든 노드를 각각의 개별 집합으로 만들어준다.
private static void makeSet(String node) {
parent.put(node, node);
rank.put(node, 0);
}
}'자료구조 및 알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 자바에서의 백 트래킹(N-Queen 문제) (0) | 2021.12.16 |
|---|---|
| [알고리즘] 자바에서의 최소 신장 트리(프림 알고리즘) (0) | 2021.12.16 |
| [알고리즘] 자바에서의 다익스트라 알고리즘(최단 경로 알고리즘) (0) | 2021.12.12 |
| [알고리즘] 자바에서의 그리디(탐욕) 알고리즘 (0) | 2021.12.10 |
| [알고리즘] 자바에서의 BFS 와 DFS (0) | 2021.12.07 |


