최단 경로 문제란?
그래프에서 두 노드를 잇는 가장 짧은 경로를 찾는 문제이다.
- 가중치 그래프 에서 간선의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적이다.
* 최단 경로 문제의 종류
- 단일 출발 및 단일 도착 최단 경로 문제(single-source and single-destination shortest path problem)
: 그래프 내의 특정 노드 u 에서 출발, 또다른 특정 노드 v 에 도착하는 가장 짧은 경로를 찾는 문제이다.
- 단일 출발 최단 경로 문제(single-source shortest path problem)
: 그래프 내의 특정 노드 u와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제이다.
예를 들어 A,B,C,D 라는 노드를 가진 그래프에서 특정 노드를 A 라고 한다면, A외 모든 노드인 B,C,D 와 A 간에 각각 가장 짧은 경로를 찾는 문제를 의미한다.(A -> B, A -> C, A -> D)
- 전체 쌍(all-pair) 최단 경로
: 그래프 내의 모든 노드 쌍(u,v) 에 대한 최단 경로를 찾는 문제이다.
다익스트라 알고리즘
- 다익스트라 알고리즘은 위의 최단 경로 문제 종류 중, 2번에 해당한다.(단일 출발 최단 경로 문제)
- 하나의 정점에서 다른 모든 정점간의 각각 가장 짧은 거리를 구하는 문제이다.
* 다익스트라 알고리즘의 로직
- 첫 정점을 기준으로 연결되어 있는 정점들을 추가해가며 최단 거리를 갱신하는 기법이다.
- 다익스트라 알고리즘은 너비 우선탐색(BFS) 과 유사하다.
- 첫 정점 부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트 하는 방식으로 진행된다.
- 다익스트라 알고리즘의 다양한 변형 로직이 있지만, 가장 개선된 우선순위 큐를 사용하는 방식에 집중하자.
* 우선순위 큐를 활용한 다익스트라 알고리즘
- 우선순위 큐는 최소 힙 방식을 활용해서 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 된다.
1. 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점 까지의 거리를 저장한다.
- 초기에는 첫 정점의 거리는 0 (자기 자신이기 때문), 나머지는 무한대로 저장한다.(inf 라고 표현함 - 아직 각 노드로 가는 거리를 모르기 때문)
- 우선순위 큐에 첫 정점 (거리 0) 만 먼저 넣는다.
2. 우선순위 큐에서 노드를 꺼낸다.
- 처음에는 첫 정점만 저장되어 있으므로 첫 정점이 꺼내진다.
- 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점 까지의 거리를 비교한다.
- 배열에 저장되어 있는 거리보다 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트 한다.
- 배열에 해당 노드의 거리가 업데이트 된 경우 우선순위 큐에 넣는다.
- 결과적으로 너비 우선탐색 방식과 유사하게 첫 정점에 인접한 노드들을 순차적으로 방문하게 된다.
- 만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다 더 긴 거리(루트) 를 가진 노드 의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않는다.
3. 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복한다.
좀 더 구체적으로 알아보자.
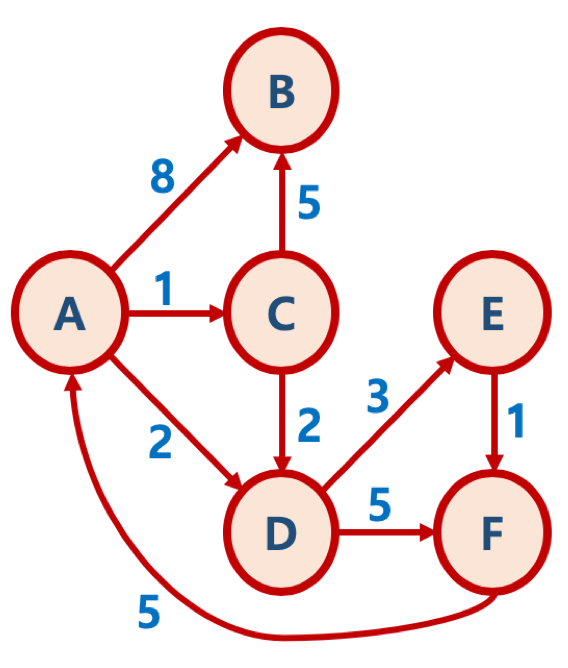
1 단계 : 초기화
첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점 까지의 거리를 저장한다.
- 초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장한다.(inf)
- 우선순위 큐에 첫 정점(거리 0) 만 먼저 넣는다.
배열
| A | B | C | D | E | F |
| 0 | inf | inf | inf | inf | inf |
우선순위 큐
| A |
| 0 |
2 단계 : 우선순위 큐에서 추출한 (A,0) - [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
우선순위 큐에서 노드를 꺼낸다. (첫 정점)
- 처음에는 첫 정점만 저장되어 있으므로 첫 정점이 꺼내진다.
- 첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
- 배열에 저장되어 있는 거리보다 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트 한다.
- 배열에 해당 노드의 거리가 업데이트 된 경우, 우선순위 큐에 넣는다.
* 이전 배열 상태에서 보듯이 첫 정점 이외엔 모두 inf 였으므로, 첫 정점에 인접한 노드들은 모두 우선순위 큐에 들어가고, 첫 정점과 인접한 노드간의 거리가 배열에 업데이트 된다.
배열
| A | B | C | D | E | F |
| 0 | 8 | 1 | 2 | inf | inf |
우선순위 큐
| C | D | B |
| 1 | 2 | 8 |
3 단계 : 우선순위 큐에서 (C,1) - [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
우선순위 큐가 최소 힙 방식이므로, 위 표에서 넣어진 (C,1), (D,2), (B,8) 중 (C,1) 이 먼저 추출된다.(pop)
위 표에서 보듯이 1단계 까지의 A - B 최단 거리는 8인 상황이다.
- A - C 까지의 거리는 1, C 에 인접한 B, D 에서 C - B 는 5, 즉 A - C - B 는 1 + 5 = 6 이므로, A - B 최단 거리 8 보다 더 작은 거리이다. 그렇기 때문에 이를 배열에 업데이트 해준다.
- 배열이 업데이트 되었으므로 B, 6 (A 에서 B 까지의 현재까지 발견된 최단 거리) 값이 우선순위 큐에 넣어진다.
- C - D 의 거리는 2, 즉 A - C - D 는 1 + 2 = 3 이므로, A - D 의 현재 최단 거리인 2보다 긴 거리이다.
그렇기 때문에 D의 거리는 업데이트 되지 않는다.
배열
| A | B | C | D | E | F |
| 0 | 6 | 1 | 2 | inf | inf |
우선순위 큐
| D | B | B |
| 2 | 6 | 8 |
4 단계 : 우선순위 큐에서 (D,2) - [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산
지금까지 접근하지 못했던 E와 F 거리가 계산된다.
- A - D 까지의 거리인 2 에 D - E 가 3 이므로 이를 더해서 E, 5
- A - D 까지의 거리인 2 에 D - F 가 5 이므로 이를 더해서 F, 7
배열
| A | B | C | D | E | F |
| 0 | 6 | 1 | 2 | 5 | 7 |
우선순위 큐
| E | B | F | B |
| 5 | 6 | 7 | 8 |
5 단계 : 우선순위 큐에서 (E, 5) - [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리를 계산한다.
A - E 거리가 5인 상태에서, E 에 인접한 F 를 가는 거리는 1, 즉 A - E - F 는 5 + 1 = 6, 현재 배열에 A - F 최단거리가 7로 기록되어 있으므로 F, 6 으로 업데이트 한다.
- 우선순위 큐에 F, 6 추가
배열
| A | B | C | D | E | F |
| 0 | 6 | 1 | 2 | 5 | 6 |
우선순위 큐
| B | F | F | B |
| 6 | 6 | 7 | 8 |
6 단계 : 우선순위 큐에서 (B, 6), (F, 6) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산
예제의 방향 그래프에서 B 노드는 다른 노드로 가는 루트가 없다.
F 노드는 A 노드로 가는 루트가 있으나, 현재 A - A 가 0 인 반면에, A - F - A 는 6 + 5 = 11, 즉 더 긴 거리이므로 업데이트 되지 않음
배열
| A | B | C | D | E | F |
| 0 | 6 | 1 | 2 | 5 | 6 |
우선순위 큐
| F | B |
| 7 | 8 |
7 단계 : 우선순위 큐에서 (F, 7), (B, 8) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산
A - F 로 가는 하나의 루트의 거리가 7 인 상황이나, 배열에서 이미 A - F 로 가는 현재의 최단 거리가 6인 루트의 값이 있는 상황이므로, 더 긴 거리인 F, 7 루트 기반 인접 노드까지의 거리는 계산할 필요가 없음
그렇기 때문에 계산없이 스킵한다.
- 계산하더라도 A - F 거리가 6인 루트보다 무조건 더 긴 거리가 나올수 밖에 없다.
B, 8 도 현재 A - B 거리가 6 이므로, 인접 노드 거리 계산이 필요없다.
* 우선순위 큐 사용 장점
- 지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산한다.
- 더 긴 거리로 계산된 루트에 대해서는 계산을 스킵 할 수 있다.
자바로 직접 작성해보자.
- Node.java
import java.util.List;
public class Node implements Comparable<Node>{
private int value;
private String nodeName;
private List<Node> connectList;
public Node(String nodeName, int value) {
this.nodeName = nodeName;
this.value = value;
}
public String getNodeName() {
return nodeName;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
public List<Node> getConnectList() {
return connectList;
}
public void setConnectList(List<Node> connectList) {
this.connectList = connectList;
}
@Override
public int compareTo(Node node) {
if(this.value > node.getValue())
return 1;
else if(this.value < node.getValue())
return -1;
return 0;
}
}
- Dijkstra.java
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
public class Dijkstra {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
System.out.println("노드 갯수 입력");
int nodeCount = Integer.parseInt(br.readLine());
Node[] nodeArray = new Node[nodeCount];
Node startNode = new Node("A", 0);
System.out.println("첫 노드 생성 완료");
for(int i = 0; i < nodeCount; i++) {
if(i == 0) {
System.out.println("첫 노드와 인접한 노드의 갯수를 입력하세요 : ");
int connectNodeCount = Integer.parseInt(br.readLine());
List<Node> connectList = new ArrayList<Node>();
for(int index = 0; index < connectNodeCount; index++) {
System.out.println("노드의 이름과 가중치를 입력하세요");
System.out.println("노드 : ");
String nodeName = br.readLine();
System.out.println("가중치 : ");
int value = Integer.parseInt(br.readLine());
Node connectNode = new Node(nodeName, value);
connectList.add(connectNode);
}
startNode.setConnectList(connectList);
nodeArray[i] = startNode;
}
else {
System.out.println();
System.out.println("새로운 노드를 생성합니다.");
System.out.println();
System.out.println("노드의 이름을 입력하세요 : ");
String nodeName = br.readLine();
System.out.println("인접한 노드의 갯수를 입력하세요 : ");
int connectNodeCount = Integer.parseInt(br.readLine());
List<Node> connectList = new ArrayList<Node>();
if(connectNodeCount != 0) {
for(int index = 0; index < connectNodeCount; index++) {
System.out.println("노드의 이름과 가중치를 입력하세요");
System.out.println("노드 : ");
String connectName = br.readLine();
System.out.println("가중치 : ");
int value = Integer.parseInt(br.readLine());
Node connectNode = new Node(connectName, value);
connectList.add(connectNode);
}
Node node = new Node(nodeName, Integer.MAX_VALUE);
node.setConnectList(connectList);
nodeArray[i] = node;
}
else {
Node node = new Node(nodeName, Integer.MAX_VALUE);
node.setConnectList(connectList);
nodeArray[i] = node;
}
}
}
PriorityQueue<Node> prior = new PriorityQueue<Node>();
prior.offer(startNode);
while(!prior.isEmpty()) {
Node currentNode = prior.poll();
List<Node> connectList = currentNode.getConnectList();
for(int i = 0; i < connectList.size(); i++) {
Node connectNode = connectList.get(i);
for(int index = 0; index < nodeArray.length; index++) {
if(nodeArray[index].getNodeName().equals(connectNode.getNodeName())) {
if(nodeArray[index].getValue() <
connectNode.getValue() + currentNode.getValue())
continue;
else {
nodeArray[index]
.setValue(connectNode.getValue() + currentNode.getValue());
prior.offer(nodeArray[index]);
}
}
}
}
}
for(int i = 0; i < nodeArray.length; i++) {
System.out.println(nodeArray[i].getNodeName() + " : " + nodeArray[i].getValue());
}
}
}
다익스트라 알고리즘의 시간복잡도
다익스트라 알고리즘은 크게 다음 두 가지 과정을 거친다.
- 과정1 : 각 노드마다 인접한 간선들을 모두 검사하는 과정
- 과정2 : 우선순위 큐에 노드/거리 정보를 넣고 삭제(pop) 하는 과정
각 과정 별 시간 복잡도
- 과정 1 : 각 노드는 최대 한번 씩 방문하므로(첫 노드와 해당 노드간의 갈 수 있는 루트가 있는 경우만 해당)
그래프의 모든 간선은 최대 한번 씩 검사한다.
- 즉, 각 노드마다 인접한 간선들을 모두 검사하는 과정은 O(E) 시간이 걸린다. E 는 간선(edge) 의 약자이다.
- 과정 2 : 우선순위 큐에 가장 많은 노드, 거리 정보가 들어있는 경우, 우선순위 큐에 노드/거리 정보를 넣고, 삭제하는 과정이 최악의 시간이 걸린다.
- 우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 시나리오는 그래프의 모든 간선이 검사될 때마다 배열의 최단 거리가 갱신되고, 우선순위 큐에 노드/거리가 추가되는 것이다.
- 이 때 추가는 각 간선마다 최대 한 번 일어날 수 있으므로, 최대 O(E) 시간이 걸리고, O(E) 개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 O(logE) 가 걸린다.
- 따라서 해당 과정의 시간 복잡도는 O(ElogE) 이다.
* 총 시간 복잡도
- 과정 1 + 과정 2 = O(E) + O(ElogE) = O(E + ElogE) = O(ElogE)
참고 : 힙의 시간복잡도
depth(트리의 높이) 를 h 라고 표기한다면 n 개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제 시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 h = log2n 에 가까우므로, 시간 복잡도는 O(log n)
'자료구조 및 알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 자바에서의 최소 신장 트리(프림 알고리즘) (0) | 2021.12.16 |
|---|---|
| [알고리즘] 자바에서의 최소 신장 트리(크루스칼 알고리즘) (0) | 2021.12.15 |
| [알고리즘] 자바에서의 그리디(탐욕) 알고리즘 (0) | 2021.12.10 |
| [알고리즘] 자바에서의 BFS 와 DFS (0) | 2021.12.07 |
| [알고리즘] 자바에서의 그래프 - 기초 (0) | 2021.12.06 |


