https://www.acmicpc.net/problem/26646
26646번: 알프스 케이블카
ALPS 부원들은 친목 도모를 위해 다 같이 알프스 산맥으로 여행을 떠났다! 알프스 산맥은 $N$개의 산이 겹치거나 빈 부분 없이 일렬로 나열된 형태이며, 왼쪽에서부터 $i$번째에 위치한 산은 빗변
www.acmicpc.net
* 문제 요약
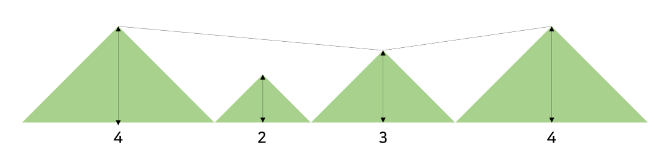
ALPS 부원들은 친목 도모를 위해 다 같이 알프스 산맥으로 여행을 떠났다! 알프스 산맥은 N개의 산이 겹치거나 빈 부분 없이 일렬로 나열된 형태이며, 왼쪽에서부터 i번째에 위치한 산은 빗변을 아래로 하며 높이가 Hi 인 직각 이등변 삼각형이다.
ALPS 부원들은 체력이 좋지 않기 때문에 1번 산에서 시작해 N번 산에서 끝나는 케이블카 노선을 설치해 산을 오르려 한다. 노선을 설치하는 법은 다음과 같다.
1. 1번 산의 정상과 다른 산의 정상을 직선으로 잇는 와이어를 설치하고, 다시 그 산의 정상에서 다른 산의 정상으로 와이어를 설치한다. 이 때 와이어는 산을 가로질러 설치 될 수 있다.
2. 이를 N번 산을 끝으로 할 때까지 자유롭게 반복한다.
각 와이어 설치 비용은 설치해야 할 와이어 길이의 제곱과 같으며 노선의, 설치 비용은 사용한 와이어의 설치 비용의 합이다. ALPS 부원들을 위해 1번 산에서 시작해 N번산에서 끝나는 노선을 설치하기 위한 최소 비용을 구해보자.
* 입력
첫 번째 줄에 알프스 산맥을 이루는 산의 수 N이 주어진다. (2 <= N <= 50,000)
두 번째 줄에 각 산의 높이 H1, H2, ... HN 이 공백으로 구분되어 정수로 주어진다. (1 <= Hi <= 100)
* 출력
1번 산에서 시작해 N번 산에서 끝나는 노선을 설치하기 위한 최소 비용을 출력한다.
* 예시

* 해결 과정
각 산이 직각 이등변 삼각형이고 겹치는 부분없이 나열되어 있다는 점에 집중해보면, 만약 어떤 산의 정상에서 바로 옆에 있는 산의 정상으로 와이어를 연결했을 때 각 산의 빗변을 밑변과 높이, 와이어를 빗변으로 하는 직각 삼각형이 만들어지기 때문에 각 와이어의 길이를 피타고라스의 원리를 통해 쉽게 구할 수 있다.
여기서 가장 중요한 포인트는 특정 산을 중간에 건너뛰고 와이어를 설치하는 것 보다, 단 하나의 산도 중간에 건너뛰지 않고 산들끼리 하나하나 정상과 정상간에 와이어를 설치해주는 것이 와이어의 길이를 쉽게 구하는 것과 동시에 총 설치 비용을 최소화 시키는 방법이 된다는 것이다.
이렇게 생각해보자. 연속된 3개의 산에 각 산의 정상과 정상 사이에 따로따로 와이어를 설치 해주자. 그 다음엔 중간에 있는 산 하나를 건너뛰고 첫 번째 산과 마지막 산 정상 사이에만 따로 와이어를 한번 더 설치해주자.
이러면 두번째 산을 건너뛰고 첫번째 산과 마지막 산 정상을 연결해준 와이어가 밑변이 되고, 각각의 산을 따로따로 연결해준 두 개의 와이어가 삼각형의 빗변이 되는 삼각형이 완성되는데, 이때 물론 각각의 산을 연결해준 와이어의 길이의 총합은 첫번째와 마지막 산 끼리만 연결해준 와이어의 길이보다 길기는 하지만 와이어 설치 비용은 각 와이어 길이를 제곱한 값과 같기 때문에 필연적으로 각 산끼리 연결해준 와이어의 설치 비용이 첫번째와 마지막 산 끼리만 연결해준 와이어의 설치 비용보다 더 저렴할 수 밖에 없다.
(하나하나 떼놓고 봤을 때 각각의 산을 따로 연결해준 와이어의 길이가 더 짧거니와, 이를 제곱해서 두 개의 값을 더한다고 해도 첫번째와 마지막 산의 와이어 길이를 제곱한 값이 훨씬 더 크다.)
그러므로 중간에 특정 산 하나를 건너뛰는 것 보다 각 산끼리 하나하나 전부 다 와이어를 연결해주는 것이 곧 와이어 설치 비용을 최소화 시키는 방법이 된다는 것이다.
* 코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
public class Main {
public static void main(String[] args) throws NumberFormatException, IOException {
new Main().solution();
}
private void solution() throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int count = Integer.parseInt(br.readLine());
int[] wire = new int[count];
String[] input = br.readLine().split(" ");
for (int i = 0; i < count; i++) {
wire[i] = Integer.parseInt(input[i]);
}
long result = 0;
for (int i = 0; i < wire.length - 1; i++) {
result += (Math.pow(wire[i], 2) * 2) + (Math.pow(wire[i + 1], 2) * 2);
}
bw.write(result + "\n");
bw.flush();
bw.close();
br.close();
}
}
현재 상황에서 최적의 해답을 선택한다. -> 각 반복마다 각 산들 사이에 설치되는 와이어의 길이 대비 설치 비용을 계산하여 결과 변수에 합산해준다.
선택된 해답이 조건을 만족하는지 검사한다. -> 반복을 모두 마칠 때까지는 전체 비용을 산정할 수 없으므로 계속 반복문을 진행해준다.
위의 과정을 통해 문제를 해결하였으므로 그리디 알고리즘 문제에 해당된다.
'코딩 테스트 > 그리디' 카테고리의 다른 글
| 백준 12915 - 대회 개최(자바 - 그리디) (0) | 2023.07.04 |
|---|---|
| 백준 27112 - 시간 외 근무 멈춰! (자바 - 그리디) (1) | 2023.06.13 |
| 백준 25947 - 선물 할인 (자바 - 그리디) (0) | 2023.06.09 |
| 백준 23561 - Young 한 에너지는 부족하다. (1) | 2023.06.09 |
| 백준 23323 - 황소 다마고치 (자바 - 그리디) (0) | 2023.06.09 |



